Peter Frase

So [Kevin Drum](http://motherjones.com/kevin-drum/2011/11/back-chessboard-and-future-human-race) and [Matt Yglesias](http://thinkprogress.org/yglesias/2011/11/17/371098/the-back-half-of-the-chessboard/) have read Erik Brynjolfsson and Andrew McAffee's *Race Against the Machine* e-book, and *both* of them managed to come away impressed by the exact argument that [I identified](http://www.peterfrase.com/2011/10/the-machines-and-us/) as the weakest part of the book's case. Namely, the belief the Moore's law---which stipulates that computer processing power increases at an exponential rate---can be extrapolated into the indefinite future. It's true that Moore's law seems to have held fairly well up to this point; and as Drum and Yglesias observe, if you keep extending it into the future, then pretty soon computing power will shoot up at an astronomically fast rate---that's just the nature of exponential functions. On this basis, Drum predicts that artificial intelligence is "going to go from 10% of a human brain to 100% of a human brain, and it's going to seem like it came from nowhere", while Yglesias more generally remarks that "we’re used to the idea of rapid improvements in information technology, but we’re actually standing on the precipice of changes that are much larger in scale than what we’ve seen thus far."

Let's revisit the problem with this argument, which I laid out in my review. The gist of it is that just because you think you're witnessing exponential progress, that doesn't mean you should expect that same rate of exponential growth to continue indefinitely. I'll turn the mic over to Charles Stross, from whom I [picked up this line of critique](http://www.antipope.org/charlie/blog-static/2007/05/shaping_the_future.html):

> __Around 1950, everyone tended to look at what the future held in terms of improvements in transportation speed.__

> But as we know now, __that wasn't where the big improvements were going to come from. The automation of information systems just weren't on the map__, other than in the crudest sense — punched card sorting and collating machines and desktop calculators.

> We can plot __a graph of computing power against time that, prior to 1900, looks remarkably similar to the graph of maximum speed against time.__ Basically it's a flat line from prehistory up to the invention, in the seventeenth or eighteenth century, of the first mechanical calculating machines. It gradually rises as mechanical calculators become more sophisticated, then in the late 1930s and 1940s it starts to rise steeply. __From 1960 onwards, with the transition to solid state digital electronics, it's been necessary to switch to a logarithmic scale to even keep sight of this graph.__

> It's worth noting that the complexity of the problems we can solve with computers has not risen as rapidly as their performance would suggest to a naive bystander. This is largely because interesting problems tend to be complex, and computational complexity rarely scales linearly with the number of inputs; we haven't seen the same breakthroughs in the theory of algorithmics that we've seen in the engineering practicalities of building incrementally faster machines.

> Speaking of engineering practicalities, I'm sure everyone here has heard of Moore's Law. __Gordon Moore of Intel coined this one back in 1965 when he observed that the number of transistor count on an integrated circuit for minimum component cost doubles every 24 months.__ This isn't just about the number of transistors on a chip, but the density of transistors. A similar law seems to govern storage density in bits per unit area for rotating media.

> As a given circuit becomes physically smaller, the time taken for a signal to propagate across it decreases — and if it's printed on a material of a given resistivity, the amount of power dissipated in the process decreases. (I hope I've got that right: my basic physics is a little rusty.) So we get faster operation, or we get lower power operation, by going smaller.

> We know that Moore's Law has some way to run before we run up against the irreducible limit to downsizing. However, it looks unlikely that we'll ever be able to build circuits where the component count exceeds the number of component atoms, so __I'm going to draw a line in the sand and suggest that this exponential increase in component count isn't going to go on forever; it's going to stop around the time we wake up and discover we've hit the nanoscale limits.__

So to summarize: transportation technology *looked* like it was improving exponentially, which caused people to extrapolate that forward into the future. Hence the futurists and science fiction writers of the 1950s envisioned a future with flying cars and voyages to other planets. But what actually happened was that transportation innovation plateaued, and a completely different area, communications, became the source of major breakthroughs. And that's because, as Stross says later in the essay, "new technological fields show a curve of accelerating progress — until it hits a plateau and slows down rapidly. It's the familiar sigmoid curve."

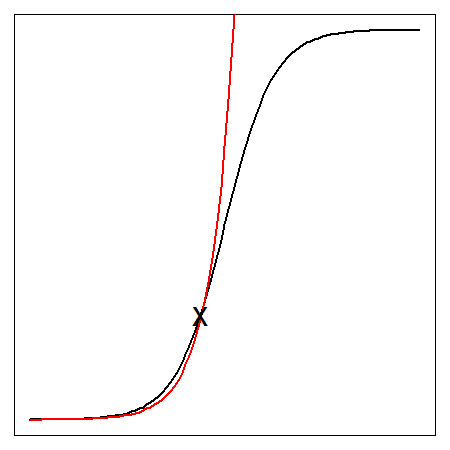
And as Stross says [elsewhere](http://www.antipope.org/charlie/blog-static/2010/05/unpleasant-medicine.html), "the first half of a sigmoid demand curve looks like an exponential function." This is what he means:

The red line in that image is an exponential function, and the black line is a sigmoid curve. Think of these as two possible paths of technological development over time. If you're somewhere around that black X mark, you won't really be able to tell which curve you're on.

But I'm inclined to agree with Stross that we're more likely to be on the sigmoid path than the exponential one, when it comes to microprocessors. That doesn't mean that we'll hit a plateau with no big technological changes at all. It's just that, as Stross says in yet [*another* place](http://www.infinityplus.co.uk/nonfiction/intcs.htm):

> New technologies slow down radically after a period of rapid change during their assimilation. However, I can see a series of overlapping sigmoid curves that might resemble an ongoing hyperbolic curve if you superimpose them on one another, each segment representing the period of maximum change as a new technology appears.

Hence economic growth *as a whole* can still look like it's [following an exponential path](http://inpp.ohiou.edu/~brune/gdp/gdp.html).

None of which is to say that I wholly reject the thesis of Brynjolfsson and McAffee's book---see the review for my thoughts on that. In a way, I think Drum and Yglesias are underselling just how weird and disruptive the future of technology will be---it's not just that it will be rapid, but that it will come in areas we can't even imagine yet. But we should be really wary of simply extending present trends into the future---our recent history of speculative economic manias should have taught us that if something [can't go on forever](http://survivalandprosperity.com/wp-content/uploads/2010/12/Shiller-Housing-Bubble-Graph.jpg), it will stop.