Deeply Dumb
July 18th, 2007 | Published in Politics, Social Science
When I was a kid, my mother had file folder labeled "deeply dumb". It was for things that went beyond ordinary, thoughtless dumbness, to reach a transcendent, awe-inspiring level of dumbness. Think motivational speakers, holistic medicine, or the men's movement.
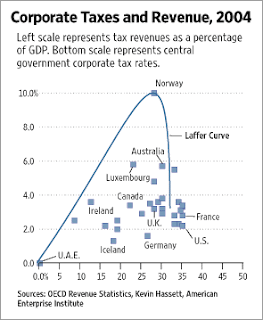
Recently I came across some of the deepest dumbness I've seen in a while. The story begins with the July 13th edition of the Wall Street Journal, which contained an editorial purporting to ratify the existence of the Laffer curve. The Laffer curve refers to the idea that the government's tax income follows a parabola: past a certain point, raising taxes will actually decrease revenue, because people will undertake less economic activity. It's a right-wing theory that nobody who isn't a conservative ideologue takes seriously, but never mind that right now. The important thing is that the editorial contained this now-immortal graph:
It should be immediately obvious that something's wrong here. But if you contemplate the graph for a while, you'll discover that there is a wealth of dumbness concealed here, a complexity of idiocy that is not apparent at first glance. It took some of the blogosphere's best minds the better part of two days to fully comprehend the depth and richness of the stupidity contained in this one image. Here is a partial reconstruction of events:
- July 13th, 12:06 AM. Mark Thoma discovers the editorial, observes that the curve does not remotely fit the data. Produces a more plausible graph, in which the line is straight and slopes upward.
- July 13th, 9:47 AM. Brad DeLong reposts Thoma's post. This one really launched the graph into blog fame. DeLong dubs it the "most dishonest WSJ editorial ever."
- July 13th, 12:25 PM. Mark Kleiman links to DeLong and Thoma. He notes that the Y-axis of the graph does not show revenues (as a laffer curve diagram normally does), but revenues as a percentage of GDP. This means that the curve must rise from 0 to 100% rather than curving down: at a 100% tax rate, by definition revenues will be 100% of GDP (Unless GDP is zero, in which case it is undefined.
- July 13th, 1:41 PM. Matthew Yglesias pronounces this "worst editorial ever".
- July 13th, 1:50 PM. Kevin Drum arrives on the scene. Notes that the steep slope of the right side of the curve implies that, if you increased Norway's corporate tax rates just 4 points, to 33 percent, revenue would fall to zero.
- July 13th, 3:03 PM. Cosmic Variance adds that the curve implies that, at tax rates above 33 percent, government revenue is actually negative.
- July 13th, 3:57 PM. Max Sawicky applies actual statistical methods to the points on the plot, gets results that look more or less like Mark Thoma's off the cuff "reality based" drawing, whether you include the outliers or not.
- July 14th, 4:35 AM. Kieran Healy take's Max's lead, uses the whole kerfuffle to make a serious social scientific point. Questions the wisdom of calling Norway an "outlier". This eventually leads to bizarre and hilarious smackdown between Healy and Megan McArdle.
- July 14th, 1:07 PM. Hilzoy at Obsidian Wings takes a new approach, realizing that the absurdity of the original curve licenses every conceivable alternative curve that could be drawn over the data. Hilarity ensues, including a proposal for unlimited government revenue and a lolcat which is actually funny. A commenter rediscovers Mark Kleiman's neglected point that the mis-specification of the Y-axis invalidates the whole exercise from the beginning.
- July 15th, 1:09 PM. Coming back around for a final pass, DeLong gets off a crack at Megan McArdle before noting that Norway is plotted in the wrong place. If oil excise taxes are accounted for correctly, then it is not an outlier at all--it falls into the same linear pattern as all the other points.
Let's recap. The editorial defended an empirically discredited theory. It plotted data points incorrectly. It drew a wholly implausible and self-serving curve over the mis-plotted data. And it specified the axes in such away that even if the Laffer curve was a reality, even if all the data points had been correct, and even if the curve they drew was a fair model of the data points, the image still would have failed to make the point it attempted to make, because the labeling of the axes was inconsistent with the argument of the Laffer curve.
It's the wisdom of crowds, people! No individual could possibly have grasped so much dumbness at once.