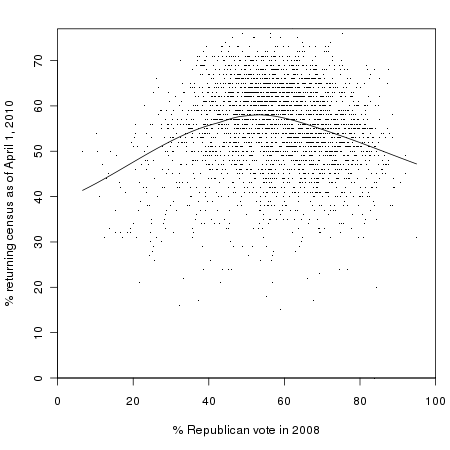
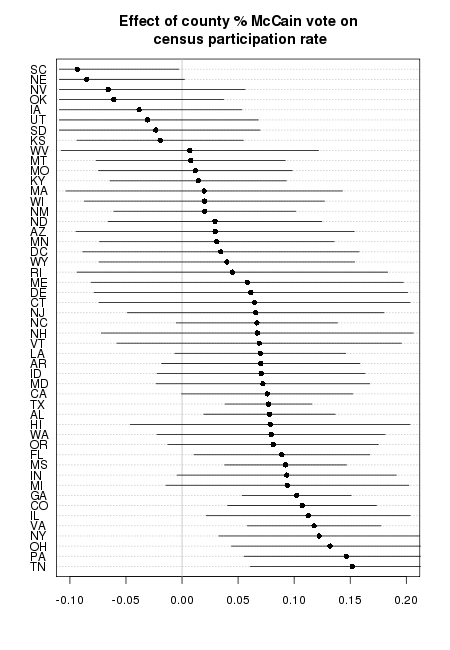
The Abuse of Statistical Significance: A Case Study
April 18th, 2010 | Published in Social Science, Statistics
For years now--decades, in fact--statisticians and social scientists have been complaining about the practice of testing for the presence of some relationship in data by running a regression and then looking to see whether some coefficient is statistically significant at some arbitrary confidence level (say, 95 percent.) And while I completely endorse these complaints, they can often seem rather abstract. Sure, you might say, the significance level is arbitrary, and you can always find a statistically significant effect with a big enough sample size, and statistical significance isn't the same as substantive importance. But as long as you're sensitive to these limitations, surely it can't hurt to use statistical significance as a quick way of checking whether you need to pay attentio to a relationship between variables, or whether it can be safely ignored?
As it turns out, a reliance on statistical significance can lead you to a conclusion that is not just imprecise or misleading, but is in fact the exact opposite of the correct answer. Until now, I've never found a really simple, clear example of this, although the stuff discussed in Andrew Gelman's "The Difference Between 'Significant' and 'Not Significant' Is Not Statistically Significant" is a good start. But now along comes Phil Birnbaum with a report of a really amazing howler of a bad result, driven entirely by misuse of statistical significance. This is going to become my go-to example of significance testing gone horribly wrong.
Birnbaum links to this article, which used a study of cricket players to argue that luck plays a big role in how people fare in the labor market. The basic argument is that cricket players do better at home than on the road, but that teams don't take this into account when deciding what players to keep for their team. The result is that some players are more likely to be dropped just because they had the bad luck to make their debut on the road.
Now, I happen to be inclined a priori to agree with this argument, at least for labor markets in general if not cricket (which I don't know anything about). And perhaps because the argument is intuitively compelling, the paper was discussed on the New York Times Freakonomics blog and on Matt Yglesias's blog. But the analysis that the authors use to make their case is entirely bogus.
Birnbaum goes into it in excellent detail, but the gist of it is as follows. They estimate a regression of the form:
In this model, Avg is your average as a cricket bowler, and HomeDebut is 1 if you debut at home, 0 if you debut on the road. We expect coefficient B to be negative--if your average is lower, you have a better chance of being dropped. But if teams are taking the home field advantage into account, coefficients C and D should be positive, indicating that teams will value the same average more if it was achieved on the road rather than at home.
And what did the authors find? C and D were indeed positive. This would suggest that teams do indeed discount high averages that were achieved at home relative to those achieved on the road. Yet the authors write:
[D]ebut location is superfluous to the retention decision. Information about debut location is individually and jointly insignificant, suggesting that these committees focus singularly on debut performance, regardless of location. This signal bias suggests that batsmen lucky enough to debut at home are more likely to do well on debut and enjoy greater playing opportunities.
How do they reach this conclusion? By noting that the coefficients for the home-debut variables are not statistically significant. But as Birnbaum points out, the magnitudes and directions of the coefficients are completely consistent with what you might expect to find if there was in fact no home-debut bias in retention decisions. And the regressions are only based on 431 observations, meaning that large standard errors are to be expected. So it's true that the confidence intervals on these coefficients include zero--but that's not the same as saying that zero is the most reasonable estimate of their true value! As the saying goes, absence of evidence is not evidence of absence. As Birnbaum says, all these authors have really shown is that they don't have enough data to properly address their question.
Birnbaum goes into all of this in much more detail. I'll just add one additional thing that makes this case especially egregious. All the regressions use "robust standard errors" to correct for heteroskedasticity. Standard error corrections like these are very popular with economists, but this is a perfect example of why I hate them. For what does the robustness-correction consist of? In general, it makes standard errors larger. This is intended to decrease the probability of a type I error, i.e., finding an effect that is not there. But by the same token, larger standard errors increase type II error, failing to find an effect that is there. And in this case, the authors used the failure to find an effect as a vindication of their argument--so rather than making the analysis more conservative -i.e., more robust to random variation and mistaken assumptions--the "robust" standard errors actually tip the scales in favor of the paper's thesis!
It's entirely possible that the authors of this paper were totally unaware of these problems, and genuinely believed their findings because they had so internalized the ideology of significance-testing. And the bloggers who publicized this study were, unfortunately, engaging in a common vice: promoting a paper whose findings they liked, while assuming that the methodology must be sound because it was done by reputable people (in this case, IMF economists.) But things like this are exactly why so many people--both inside and outside the academy--are instinctively distrustful of quantitative research. And the fact that Phil Birnbaum dug this up exemplifies what I love about amateur baseball statisticians, who tend to be much more flexible and open minded in their approach to quantitative methods. I suspect a lot of trained social scientists would have read over this thing without giving it a second though.